Довольно часто во время дискуссии один говорит одно, и это кажется убедительным. Другой говорит прямо противоположное, и тоже вроде бы прав. Голова кругом идет, и часто становишься на сторону того, кто говорит более эмоционально, а не более убедительно.

Можно допустить ошибку. Кроме того, если я, возражая кому-нибудь, не принимаю его утверждения, то все-таки кое-что могу признать истинным. Например, я не согласен с тем, что «все люди мудры», и отрицаю это, но я могу признать, что «некоторые люди мудры». Эти два суждения совместимы друг с другом. «Все люди смертны» и «Некоторые люди не суть смертны» несовместимы.
Противоположность суждений исследуется по правилу логического квадрата (рис. 1)
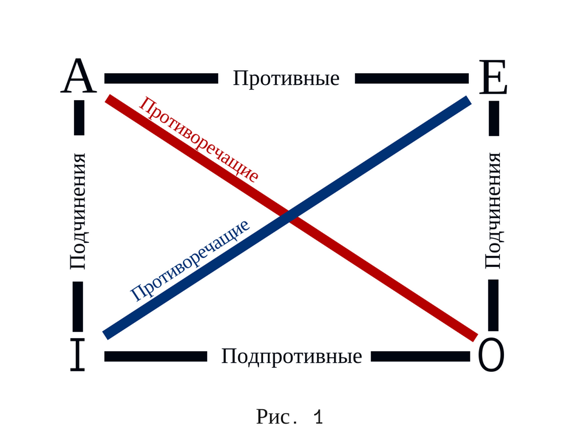
Противоречие (А-О, Е-I). Если А ложно, то О истинно («все люди искренни» —«некоторые люди неискренни»). Из двух противоречащих суждений при истинности одного суждения другое оказывается ложным. Из этого следует, что из двух противоречащих суждений одно должно быть истинным, а другое ложным. Два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными. Вот действие закона исключенного третьего. Если нужно доказать ложность суждения «Все люди искренни», то достаточно найти одного неискреннего человека. Те самым я обосную положение, что некоторые люди неискренни. А отсюда вытекает ложность суждения «все люди искренни» и нет необходимости проводить длительные эксперименты на большом количестве людей.
Противность (А-Е). Из двух противных суждений из истинности одного следует ложность другого, но из ложности одного не следует истинность другого; оба суждения не могут быть одновременно истинными, но оба могут быть ложными. Здесь мы видим действие второго закона логики.
Подчинение(А-I, Е-О). Истинность частного суждения находится в зависимости от истинности общего суждения, но не наоборот.
ПодпротивностьО-О). Оба подпротивных суждения могут быть одновременно истинными, но не могут быть одновременно ложными.
Наибольшая противоположность (диаметральная), А-Е но при опровержении А и Е удобнее пользоваться О и I.
А теперь давайте пройдемся по логическому квадрату.
Тем, кто хочет всерьез освоить логику, предлагаю в каждой строчке оставить открытыми первые три слова, остальное закрыть листом бумаги, дописать каждую строчку, а потом сверить это с тем, что напечатано (рис. 2).









